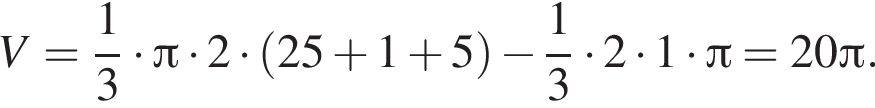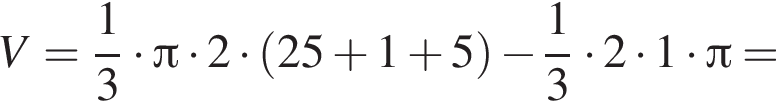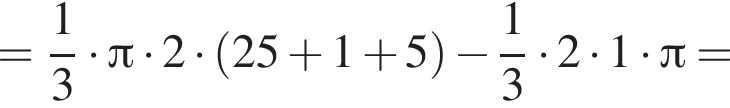На координатной прямой отмечены точки А, В, С, D, F. Числу ![]() на координатной прямой может соответствовать точка:
на координатной прямой может соответствовать точка:
Централизованное тестирование по математике, 2019
Даны системы неравенств. Укажите номер системы неравенств, которая равносильна системе неравенств 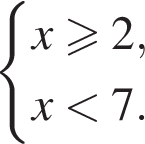
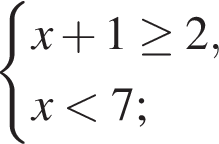
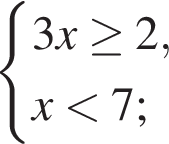
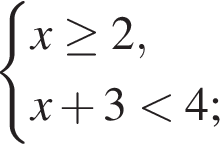
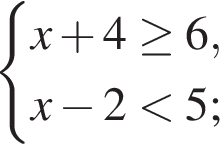
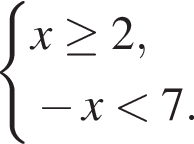
Укажите номер верного утверждения:
1) 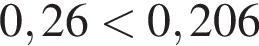
2) 
3) 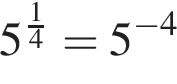
4) 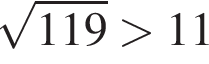
5) 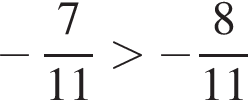
Найдите градусную меру угла, смежного с углом, радианная мера которого равна ![]()
Укажите результат разложения многочлена cx + cy − (x + y)2
а) 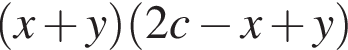
б) 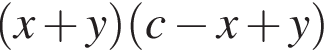
в) 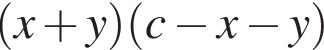
г) 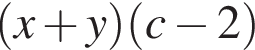
д) 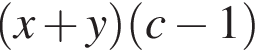
Окружность задана уравнением  Укажите верное утверждения.
Укажите верное утверждения.
 проходит через центр окружности
проходит через центр окружностиТочка A находится в узле сетки (см.рис).
Если точка B симметрична точке А относительно начала координат, то длина отрезка АВ равна:
Через точку А к окружности с центром в точке О проведены касательные АВ и АС, где В и С — точки касания. Найдите градусную меру угла ВАС, если

От пристани одновременно отправляются по течению реки катер(I) и против течения реки моторная лодка (II). На рисунке приведены графики их движения. Определите скорость течения реки (в км/ч), если катер и моторная ложка имеют одинаковые собственные скорости.
Пусть x1 и x2 — корни уравнения 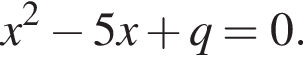 Найдите число q, при котором выполняется равенство
Найдите число q, при котором выполняется равенство 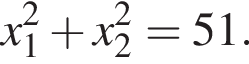
Cумма первых четырех членов геометрической прогрессии равна 45, знаменатель прогрессии равен 2. Найдите второй член геометрической прогрессии.
В треугольнике ABC 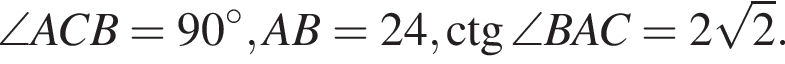 Найдите длину стороны CB.
Найдите длину стороны CB.
Укажите номера уравнений, которые не имеют действительных корней.
1) 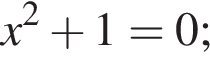
2) 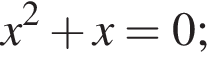
3) 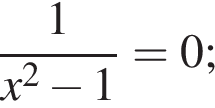
4) 
5) 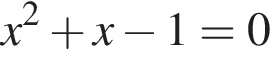
В ботаническом саду разбили клумбу треугольной формы. Длина первой стороны клумбы равна 6 м, длина второй стороны в 2,5 раза больше длины первой, а длина третьей составляет не меньше 120% от длины второй стороны. Какому условию должен удовлетворять периметр Р (в метрах) этой клумбы.
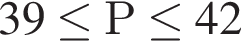
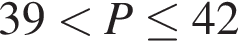


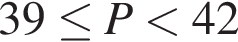
Найдите сумму всех натуральных чисел n, для которых выполняется равенство НОК(n,147) = 147.
Секущая плоскость пересекает сферу по окружности, радиус которой равен 3. Если расстояние от центра сферы до секущей плоскости равно 6, то площадь сферы равна:
Вычислите сумму наибольшего отрицательного и наименьшего положительного корней уравнения
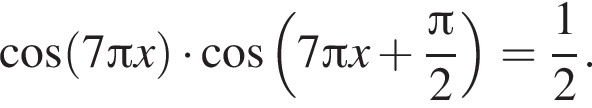
ABCA1B1C1 — правильная треугольная призма, все ребра которой равны
![]() Точки P и K — середины ребер B1C1 и BB1 соответственно,
Точки P и K — середины ребер B1C1 и BB1 соответственно, 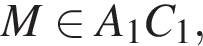
 Найдите длину отрезка, по которому плоскость, проходящая через M, P, K, пересекает грань AA1C1C.
Найдите длину отрезка, по которому плоскость, проходящая через M, P, K, пересекает грань AA1C1C.
Для начала каждого из предложений подберите его окончание 1−5 так, чтобы получилось верное утверждение.
A) Значение выражения 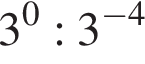 равно:
равно:
Б) Значение выражения 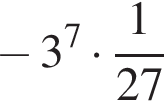 равно:
равно:
В) Значение выражения  равно:
равно:
1) 9
2) −81
3) ![]()
4) ![]()
5) 81
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Выберите три верных утверждения, если известно, что прямая а перпендикулярна плоскости
![]() и пересекает ее в точке О.
и пересекает ее в точке О.
1) Если прямая b параллельная прямой а, то она перпендикулярная плоскости ![]()
2) Любая прямая, перпендикулярная прямой а и проходящая через току О лежит в плоскости ![]()
3) Существует единственная прямая, параллельная прямой а и перпендикулярная плоскости ![]()
4) Любая прямая, перпендикулярная прямой а, лежит в плоскости ![]()
5) Через прямую а проходит единственная плоскость, перпендикулярная плоскости ![]()
Существует множество плоскостей, перпендикулярных прямой а.
6) Существует множество плоскостей, перпендикулярных прямой а.
Ответ запишите в виде последовательности цифр в порядке возрастания. Например: 123.
В двух сосудах 38 литров жидкости. Если 5% жидкости из первого сосуда перелить во второй, то в обоих сосудах окажется одинаковое количество жидкости. Сколько литров жидкости было во втором сосуде первоначально?
Найдите сумму корней (корень, если он единственный) уравнения 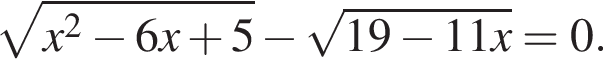
В трапеции ABCD с основаниями AD > BC точка пересечения ее диагоналей делит диагональ AC на отрезки 6 и 3. Найдите площадь трапеции, если площадь треугольника ABC равна 12.
Найдите произведение наибольшего целого решения на количество всех целых решений неравенства 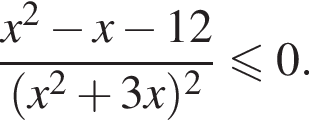
Функция y = f(x) определена на множестве действительных чисел ![]() является нечетной, периодической с периодом T = 26 и при
является нечетной, периодической с периодом T = 26 и при  задается формулой
задается формулой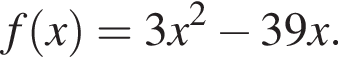 Найдите произведение абсцисс точек пересечения прямой y = 36 и графика функции y = f(x) на промежутке [ −33; 15].
Найдите произведение абсцисс точек пересечения прямой y = 36 и графика функции y = f(x) на промежутке [ −33; 15].
В основании пирамиды лежит прямоугольный треугольник, длина гипотенузы которого равна 6, острый угол равен 60°. Каждая боковая грань пирамиды наклонена к плоскости основания под углом, равным 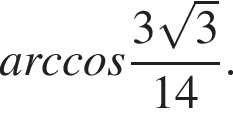 Найдите площадь боковой поверхности пирамиды.
Найдите площадь боковой поверхности пирамиды.
Найдите увеличенную в 3 раза сумму квадратов корней уравнения 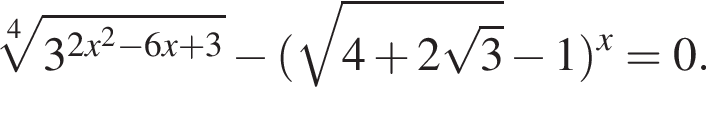
Найдите сумму всех целых чисел из области определения функции 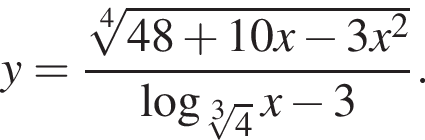
Двое рабочих различной квалификации выполнили некоторую работу, причем первый проработал 4 часа, а затем к нему присоединился второй. Если бы сначала второй рабочий работал 4 ч, а зачем к нему присоединился первый, то работы была бы закончена на 48 мин позже. Известно, что первый рабочий восьмую часть работы выполняет на 3 часа быстрее, чем второй рабочий выполняет шестую часть работы. Сколько минут заняло выполнение всех работы?
Прямоугольный треугольник, длина гипотенузы которого равна 5, высота, проведенная к ней равна 2, вращается вокруг прямой, перпендикулярной гипотенузе и проходящей в плоскости треугольника через вершину большего острого угла. Найдите объем V тела вращения и в ответ запишите значение выражения ![]()

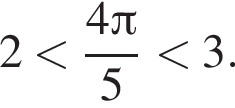 Таким образом, точка B может соответствовать этому числу.
Таким образом, точка B может соответствовать этому числу.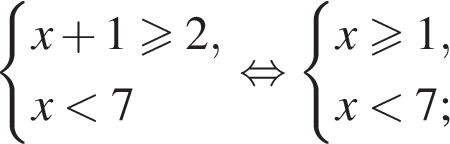
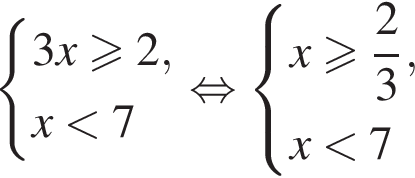
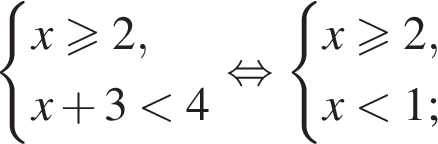
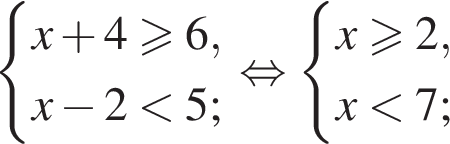
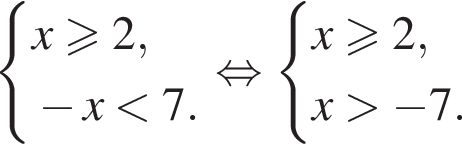
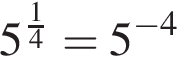 — неверно;
— неверно;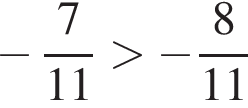 — верно.
— верно.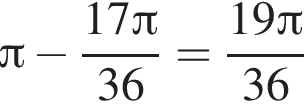 или 95°.
или 95°.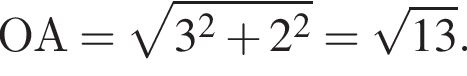
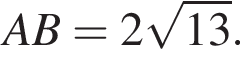
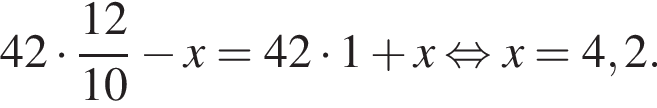
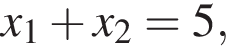 а
а 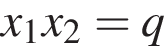
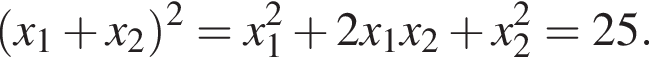 Зная то, что
Зная то, что 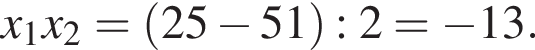
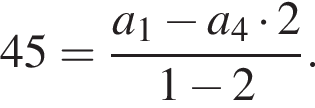 Подставим формулу четвертого члена
Подставим формулу четвертого члена 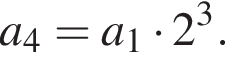 Имеем:
Имеем: 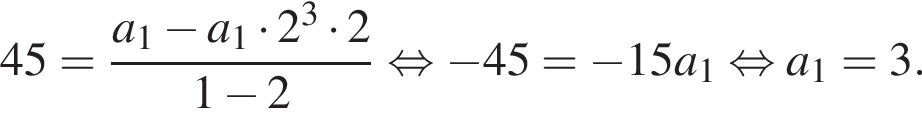
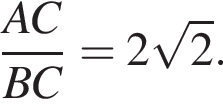 Из теоремы Пифагора:
Из теоремы Пифагора: Подставим одно выражение в другое и решим уравнение:
Подставим одно выражение в другое и решим уравнение: 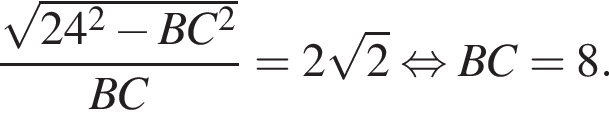
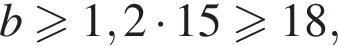 а также
а также 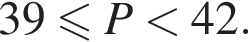
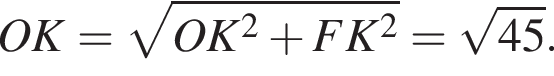 Таким образом, OK = R =
Таким образом, OK = R = 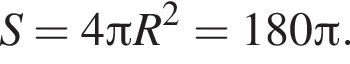
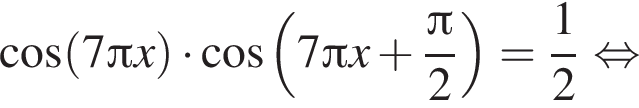

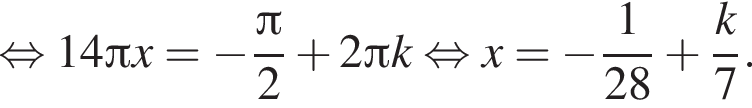


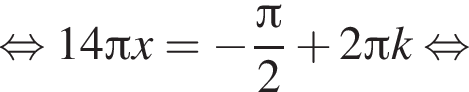
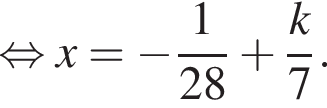
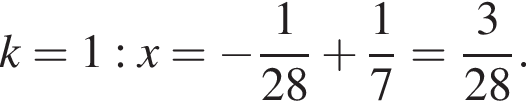
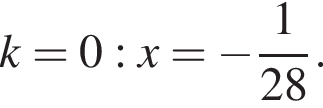
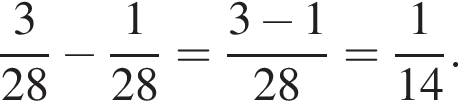
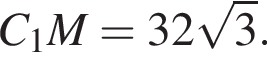
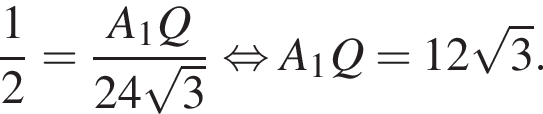
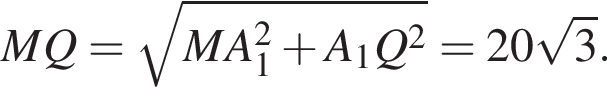
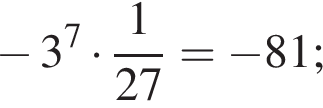
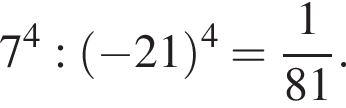
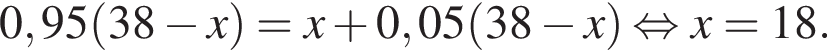
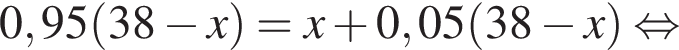

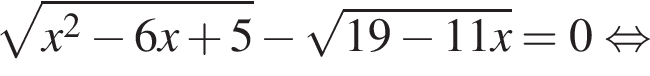
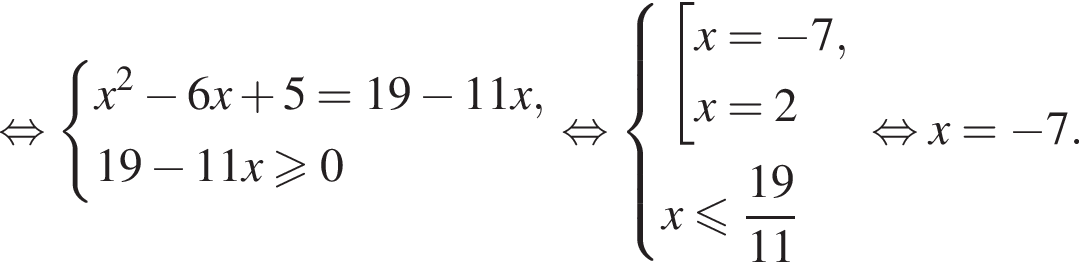
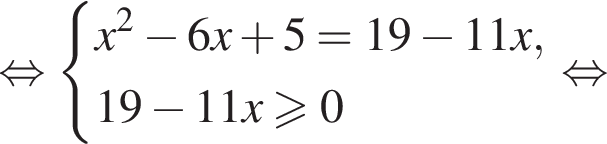
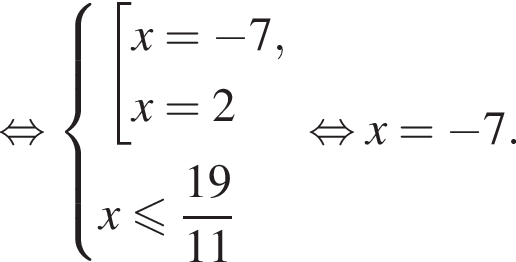
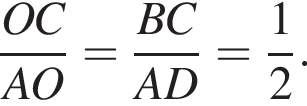
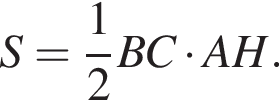 Тогда
Тогда  Таким образом,
Таким образом, 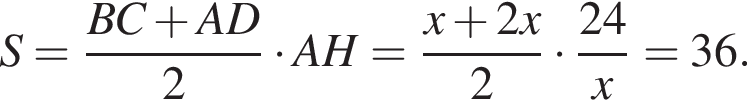
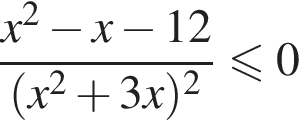
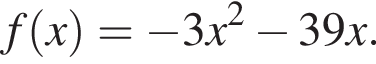 Данный интервал входит в промежуток, на котором необходимо найти произведение абсцисс. Найдем абсциссы точек пересечения полученной функции и прямой y = 36.
Данный интервал входит в промежуток, на котором необходимо найти произведение абсцисс. Найдем абсциссы точек пересечения полученной функции и прямой y = 36. 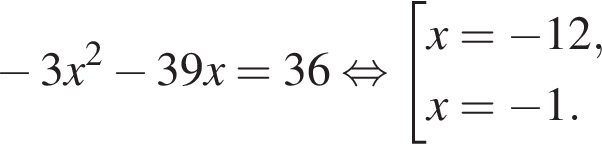
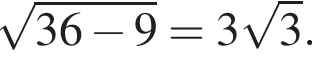 Тогда площадь основания равна
Тогда площадь основания равна 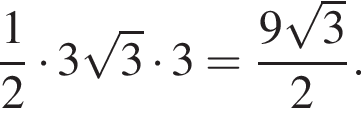
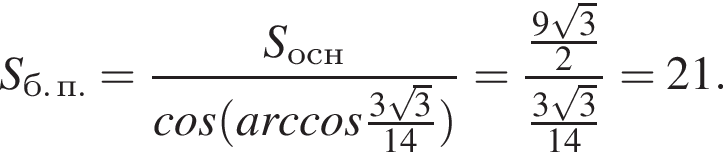
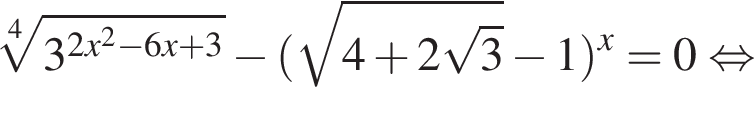
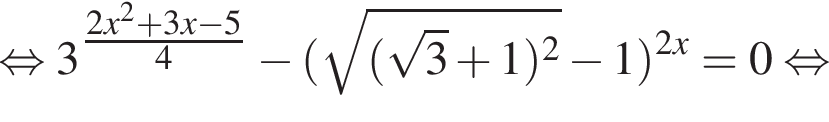
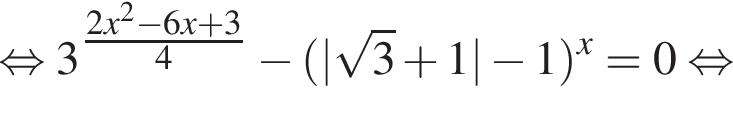
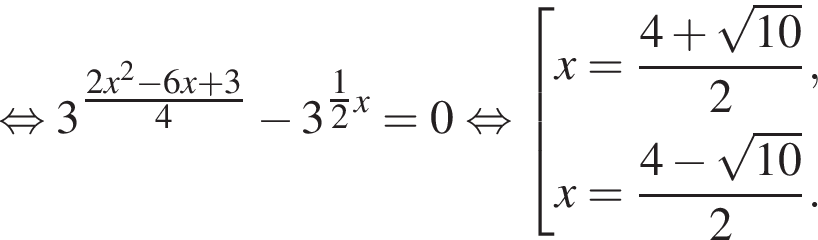
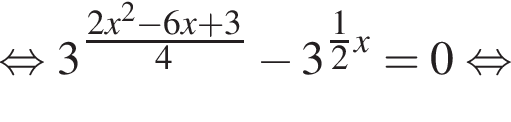
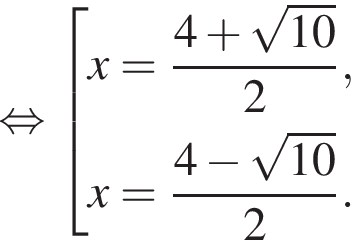
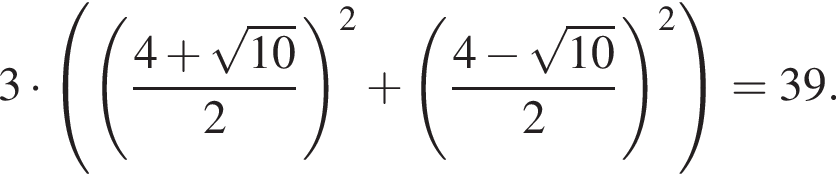
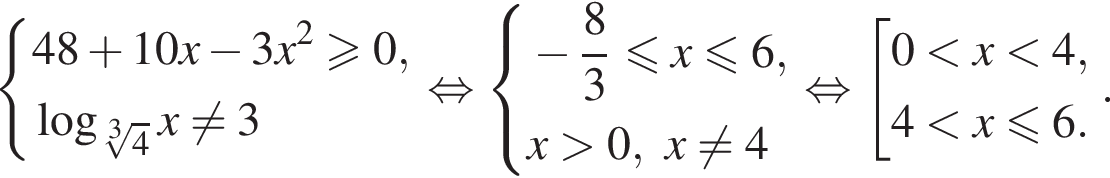
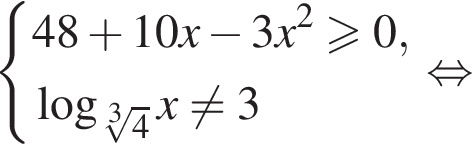
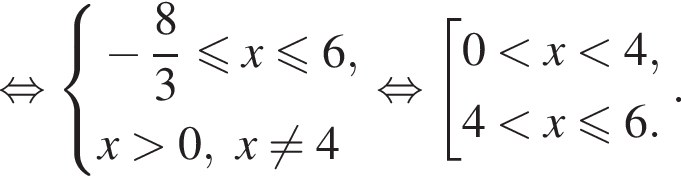
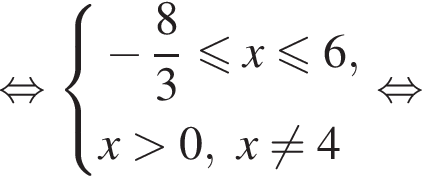
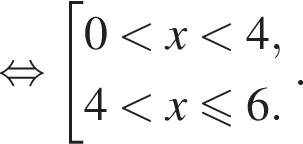
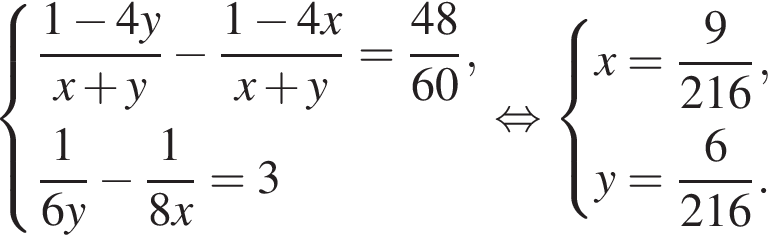
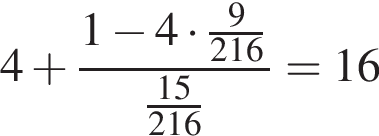 часов или 960 минут.
часов или 960 минут.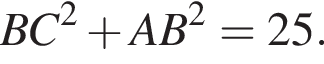 Площадь треугольника, с одной стороны, равна половине произведения катетов, а с другой — половина произведения высоты на сторону, к которой проведена высота. Имеем:
Площадь треугольника, с одной стороны, равна половине произведения катетов, а с другой — половина произведения высоты на сторону, к которой проведена высота. Имеем: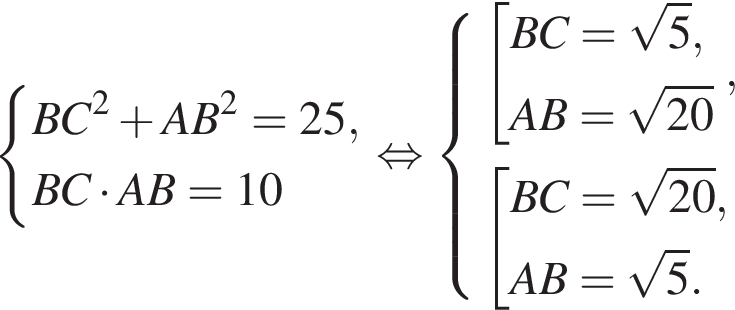
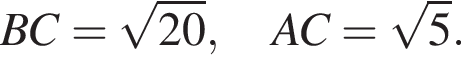 По теореме Пифагора найдем
По теореме Пифагора найдем